|
CVM Class Library
8.1
This C++ class library encapsulates concepts of vector and different matrices including square, band, symmetric and hermitian ones in Euclidean space of real and complex numbers.
|
|
CVM Class Library
8.1
This C++ class library encapsulates concepts of vector and different matrices including square, band, symmetric and hermitian ones in Euclidean space of real and complex numbers.
|
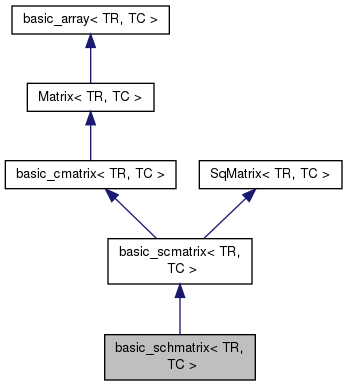
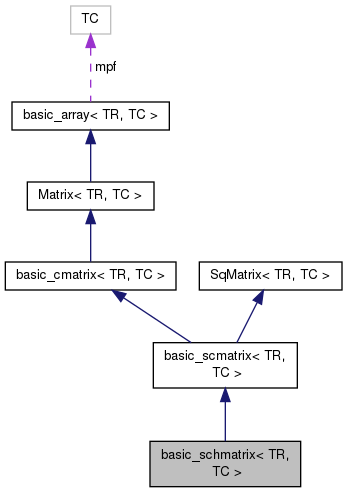
End-user class encapsulating hermitian matrix of complex numbers. More...
#include <cvm.h>
Public Member Functions | |
| basic_schmatrix () | |
| Default constructor. | |
| basic_schmatrix (tint nDim) | |
| Constructor. | |
| basic_schmatrix (TC *pd, tint nDim, TR tol=basic_cvmMachSp< TR >()) | |
| Constructor. | |
| basic_schmatrix (const TC *pd, tint nDim, TR tol=basic_cvmMachSp< TR >()) | |
| Constructor. | |
| basic_schmatrix (const basic_schmatrix &m) | |
| Copy constructor. | |
| basic_schmatrix (basic_schmatrix &&m) noexcept | |
| Move constructor. | |
| basic_schmatrix (const BaseCMatrix &m, TR tol=basic_cvmMachSp< TR >()) | |
| Constructor. | |
| basic_schmatrix (const RVector &v) | |
| Constructor. | |
| basic_schmatrix (const basic_srsmatrix< TR > &m) | |
| Constructor. | |
| basic_schmatrix (const TR *pRe, const TR *pIm, tint nDim, TR tol=basic_cvmMachSp< TR >()) | |
| Constructor. | |
| basic_schmatrix (const basic_srmatrix< TR > &mRe, const basic_srmatrix< TR > &mIm, TR tol=basic_cvmMachSp< TR >()) | |
| Constructor. | |
| basic_schmatrix (basic_schmatrix &m, tint nRowCol, tint nDim) | |
| Submatrix constructor. | |
| TC | operator() (tint nRow, tint nCol) const throw (cvmexception) |
| Value of element (not l-value) | |
| const CVector | operator() (tint nCol) const throw (cvmexception) |
| Column as not l-value. | |
| const CVector | operator[] (tint nRow) const throw (cvmexception) |
| Row as not l-value. | |
| const CVector | diag (tint nDiag) const throw (cvmexception) |
| Diagonal (not l-value) | |
| const basic_srsmatrix< TR > | real () const |
| Real part (not l-value) | |
| const basic_srmatrix< TR > | imag () const |
| Imaginary part (not l-value) | |
| basic_schmatrix & | operator= (const basic_schmatrix &m) throw (cvmexception) |
| Assignment operator. | |
| basic_schmatrix & | operator= (basic_schmatrix &&m) throw (cvmexception) |
| Move assignment operator. | |
| basic_schmatrix & | assign (const CVector &v, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Vector (as array) assignment. | |
| basic_schmatrix & | assign (const TC *pd, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| External array assignment. | |
| basic_schmatrix & | assign (tint nRowCol, const basic_schmatrix &m) throw (cvmexception) |
| Assignment to submatrix. | |
| basic_schmatrix & | set (tint nRow, tint nCol, TC c) throw (cvmexception) |
| Sets both elements to keep matrix hermitian. | |
| basic_schmatrix & | set_diag (tint nDiag, const CVector &vDiag) throw (cvmexception) |
| Sets lower and upper diagonals. | |
| basic_schmatrix & | set_main_diag (const RVector &vDiag) throw (cvmexception) |
| Sets main diagonal. | |
| basic_schmatrix & | assign_real (const basic_srsmatrix< TR > &mRe) throw (cvmexception) |
| Assigns real symmetric matrix to real part. | |
| basic_schmatrix & | set_real (TR d) |
| Sets all real parts to one value. | |
| basic_schmatrix & | resize (tint nNewDim) throw (cvmexception) |
| Changes dimension. | |
| bool | operator== (const basic_schmatrix &m) const |
| Matrix comparison. | |
| bool | operator!= (const basic_schmatrix &m) const |
| Matrix comparison. | |
| basic_schmatrix & | operator<< (const basic_schmatrix &m) throw (cvmexception) |
| Matrix replacement. | |
| basic_schmatrix | operator+ (const basic_schmatrix &m) const throw (cvmexception) |
| Addition operator. | |
| basic_schmatrix | operator- (const basic_schmatrix &m) const throw (cvmexception) |
| Subtraction operator. | |
| basic_schmatrix & | sum (const basic_schmatrix &m1, const basic_schmatrix &m2) throw (cvmexception) |
| Sum of matrices. | |
| basic_schmatrix & | diff (const basic_schmatrix &m1, const basic_schmatrix &m2) throw (cvmexception) |
| Difference of matrices. | |
| basic_schmatrix & | operator+= (const basic_schmatrix &m) throw (cvmexception) |
| Increment operator. | |
| basic_schmatrix & | operator-= (const basic_schmatrix &m) throw (cvmexception) |
| Decrement operator. | |
| basic_schmatrix | operator- () const |
| Unary minus operator. | |
| basic_schmatrix & | operator++ () |
| Plus identity, prefix. | |
| basic_schmatrix | operator++ (int) |
| Plus identity, postfix. | |
| basic_schmatrix & | operator-- () |
| Minus identity, prefix. | |
| basic_schmatrix | operator-- (int) |
| Minus identity, postfix. | |
| basic_schmatrix | operator* (TR dMult) const |
| Multiply by real number operator. | |
| basic_schmatrix | operator/ (TR dDiv) const throw (cvmexception) |
| Divide by real number operator. | |
| BaseSCMatrix | operator* (TC cMult) const |
| Multiply by complex number operator. | |
| BaseSCMatrix | operator/ (TC cDiv) const throw (cvmexception) |
| Divide by complex number operator. | |
| basic_schmatrix & | operator*= (TR dMult) |
| Multiply by real number and assign. | |
| basic_schmatrix & | operator/= (TR dDiv) throw (cvmexception) |
| Divide by real number and assign. | |
| basic_schmatrix & | normalize () |
| Matrix normalizer. | |
| basic_schmatrix | operator! () const throw (cvmexception) |
| Matrix transposition. | |
| basic_schmatrix | operator~ () const |
| Does nothing and returns copy of calling hermitian matrix. | |
| basic_schmatrix & | transpose (const basic_schmatrix &m) throw (cvmexception) |
| Matrix transposition. | |
| basic_schmatrix & | conj (const basic_schmatrix &m) throw (cvmexception) |
Assigns hermitian matrix m to calling one and returns reference to the matrix changed. | |
| basic_schmatrix & | transpose () throw (cvmexception) |
| Matrix transposition (in-place) | |
| basic_schmatrix & | conj () |
| Does nothing and returns reference to calling symmetric matrix. | |
| CVector | operator* (const CVector &v) const throw (cvmexception) |
| Matrix-vector product. | |
| BaseCMatrix | operator* (const BaseCMatrix &m) const throw (cvmexception) |
| Matrix-matrix product. | |
| BaseSCMatrix | operator* (const BaseSCMatrix &m) const throw (cvmexception) |
| Matrix-matrix product. | |
| CVector | operator/ (const CVector &v) const throw (cvmexception) |
| Linear solver operator. | |
| basic_schmatrix & | herk (TR alpha, const CVector &v, TR beta) throw (cvmexception) |
| Rank-1 update matrix-vector operation. | |
| basic_schmatrix & | herk (bool bTransp, TR alpha, const BaseCMatrix &m, TR beta) throw (cvmexception) |
| Rank-1 update matrix-matrix operation. | |
| basic_schmatrix & | her2k (TC alpha, const CVector &v1, const CVector &v2, TR beta) throw (cvmexception) |
| Rank-1 update matrix-vector operation. | |
| basic_schmatrix & | her2k (bool bTransp, TC alpha, const BaseCMatrix &m1, const BaseCMatrix &m2, TR beta) throw (cvmexception) |
| Rank-1 update matrix-matrix operation. | |
| basic_schmatrix & | inv (const basic_schmatrix &m) throw (cvmexception) |
| Matrix inversion. | |
| basic_schmatrix | inv () const throw (cvmexception) |
| Matrix inversion. | |
| basic_schmatrix & | exp (const basic_schmatrix &m, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Matrix exponent. | |
| basic_schmatrix | exp (TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Matrix exponent. | |
| basic_schmatrix & | polynom (const basic_schmatrix &m, const RVector &v) throw (cvmexception) |
| Matrix polynomial. | |
| basic_schmatrix | polynom (const RVector &v) const |
| Matrix polynomial. | |
| RVector | eig (BaseSCMatrix &mEigVect) const throw (cvmexception) |
| Eigenvalues and eigenvectors. | |
| RVector | eig () const throw (cvmexception) |
| Eigenvalues. | |
| BaseSCMatrix | cholesky () const throw (cvmexception) |
| Cholesky factorization. | |
| BaseSCMatrix | bunch_kaufman (tint *nPivots) const throw (cvmexception) |
| Bunch-Kaufman factorization. | |
| basic_schmatrix & | identity () |
| Identity matrix. | |
| basic_schmatrix & | vanish () |
| Set matrix to zero. | |
| basic_schmatrix & | randomize_real (TR dFrom, TR dTo) |
| Randomizer (real part) | |
| basic_schmatrix & | randomize_imag (TR dFrom, TR dTo) |
| Randomizer (imaginary part) | |
| TR | norminf () const override |
| Infinity norm. | |
| bool | is_positive_definite () const |
| Is calling hermitian matrix positive definite? | |
| bool | equilibrate (basic_rvector< TR > &vScalings, CVector &vB) throw (cvmexception) |
| Matrix equilibration. | |
| bool | equilibrate (basic_rvector< TR > &vScalings, BaseCMatrix &mB) throw (cvmexception) |
| Matrix equilibration. | |
 Public Member Functions inherited from basic_scmatrix< TR, TC > Public Member Functions inherited from basic_scmatrix< TR, TC > | |
| basic_scmatrix () | |
| Default constructor. | |
| basic_scmatrix (tint nDim) | |
| Constructor. | |
| basic_scmatrix (TC *pd, tint nDim) | |
| Constructor. | |
| basic_scmatrix (const TC *pd, tint nDim) | |
| Constructor. | |
| basic_scmatrix (const basic_scmatrix &m) | |
| Copy constructor. | |
| basic_scmatrix (basic_scmatrix &&m) noexcept | |
| Move constructor. | |
| basic_scmatrix (const BaseCMatrix &m) | |
| Constructor. | |
| basic_scmatrix (const CVector &v) | |
| Constructor. | |
| basic_scmatrix (const basic_srmatrix< TR > &m, bool bRealPart=true) | |
| Constructor. | |
| basic_scmatrix (const TR *pRe, const TR *pIm, tint nDim) | |
| Constructor. | |
| basic_scmatrix (const basic_srmatrix< TR > &mRe, const basic_srmatrix< TR > &mIm) | |
| Constructor. | |
| basic_scmatrix (BaseCMatrix &m, tint nRow, tint nCol, tint nDim) | |
| Submatrix constructor. | |
| type_proxy< TC, TR > | operator() (tint nRow, tint nCol) throw (cvmexception) |
| Reference to element (l-value) | |
| CVector | operator() (tint nCol) throw (cvmexception) |
| Column as l-value. | |
| CVector | operator[] (tint nRow) throw (cvmexception) |
| Row as l-value. | |
| basic_scmatrix & | operator= (const basic_scmatrix &m) throw (cvmexception) |
| Assignment operator. | |
| basic_scmatrix & | operator= (basic_scmatrix &&m) throw (cvmexception) |
| Move assignment operator. | |
| basic_scmatrix & | assign (const CVector &v) throw (cvmexception) |
| Vector (as array) assignment. | |
| basic_scmatrix & | assign (const TC *pd) |
| External array assignment. | |
| basic_scmatrix & | assign (tint nRow, tint nCol, const BaseCMatrix &m) throw (cvmexception) |
| Assignment to submatrix. | |
| basic_scmatrix & | set (TC c) |
| Sets all elements to one value. | |
| basic_scmatrix & | assign_real (const basic_srmatrix< TR > &mRe) throw (cvmexception) |
| Assignment to real parts. | |
| basic_scmatrix & | assign_imag (const basic_srmatrix< TR > &mIm) throw (cvmexception) |
| Assignment to imaginary parts. | |
| basic_scmatrix & | set_imag (TR d) |
| Sets all imaginary parts to one value. | |
| basic_scmatrix & | operator<< (const basic_scmatrix &m) throw (cvmexception) |
| Matrix replacement. | |
| basic_scmatrix | operator+ (const basic_scmatrix &m) const throw (cvmexception) |
| Addition operator. | |
| basic_scmatrix | operator- (const basic_scmatrix &m) const throw (cvmexception) |
| Subtraction operator. | |
| basic_scmatrix & | sum (const basic_scmatrix &m1, const basic_scmatrix &m2) throw (cvmexception) |
| Sum of matrices. | |
| basic_scmatrix & | diff (const basic_scmatrix &m1, const basic_scmatrix &m2) throw (cvmexception) |
| Difference of matrices. | |
| basic_scmatrix & | operator+= (const basic_scmatrix &m) throw (cvmexception) |
| Increment operator. | |
| basic_scmatrix & | operator-= (const basic_scmatrix &m) throw (cvmexception) |
| Decrement operator. | |
| basic_scmatrix & | operator*= (TC cMult) |
| Multiply by complex number and assign. | |
| basic_scmatrix & | operator/= (TC cDiv) |
| Divide by complex number and assign. | |
| basic_scmatrix & | transpose (const basic_scmatrix &m) throw (cvmexception) |
| Matrix transposition. | |
| basic_scmatrix & | conj (const basic_scmatrix &m) throw (cvmexception) |
| Matrix conjugation. | |
| basic_scmatrix | operator* (const basic_scmatrix &m) const throw (cvmexception) |
| Matrix-matrix product. | |
| basic_scmatrix & | operator*= (const basic_scmatrix &m) throw (cvmexception) |
| Matrix-matrix product with assignment. | |
| basic_scmatrix & | swap_rows (tint n1, tint n2) throw (cvmexception) |
| Rows swap. | |
| basic_scmatrix & | swap_cols (tint n1, tint n2) throw (cvmexception) |
| Columns swap. | |
| CVector | solve (const CVector &vB, TR &dErr) const throw (cvmexception) |
| Linear solver. | |
| CVector | solve_tran (const CVector &vB, TR &dErr) const throw (cvmexception) |
| Linear solver (transposed) | |
| CVector | solve_conj (const CVector &vB, TR &dErr) const throw (cvmexception) |
| Linear solver (hermitian conjugated) | |
| CVector | solve (const CVector &vB) const throw (cvmexception) |
| Linear solver. | |
| CVector | solve_tran (const CVector &vB) const throw (cvmexception) |
| Linear solver (transposed) | |
| CVector | solve_conj (const CVector &vB) const throw (cvmexception) |
| Linear solver (hermitian conjugated) | |
| BaseCMatrix | solve (const BaseCMatrix &mB, TR &dErr) const throw (cvmexception) |
| Linear solver. | |
| BaseCMatrix | solve_tran (const BaseCMatrix &mB, TR &dErr) const throw (cvmexception) |
| Linear solver (transposed) | |
| BaseCMatrix | solve_conj (const BaseCMatrix &mB, TR &dErr) const throw (cvmexception) |
| Linear solver (hermitian conjugated) | |
| BaseCMatrix | solve (const BaseCMatrix &mB) const throw (cvmexception) |
| Linear solver. | |
| BaseCMatrix | solve_tran (const BaseCMatrix &mB) const throw (cvmexception) |
| Linear solver (transposed) | |
| BaseCMatrix | solve_conj (const BaseCMatrix &mB) const throw (cvmexception) |
| Linear solver (hermitian conjugated) | |
| CVector | operator% (const CVector &vB) const throw (cvmexception) |
| Linear solver operator (transposed) | |
| CVector | solve_lu (const basic_scmatrix &mLU, const tint *pPivots, const CVector &vB, TR &dErr) const throw (cvmexception) |
| LU factorization based linear solver. | |
| CVector | solve_lu (const basic_scmatrix &mLU, const tint *pPivots, const CVector &vB) const throw (cvmexception) |
| LU factorization based linear solver. | |
| BaseCMatrix | solve_lu (const basic_scmatrix &mLU, const tint *pPivots, const BaseCMatrix &mB, TR &dErr) const throw (cvmexception) |
| LU factorization based linear solver. | |
| BaseCMatrix | solve_lu (const basic_scmatrix &mLU, const tint *pPivots, const BaseCMatrix &mB) const throw (cvmexception) |
| LU factorization based linear solver. | |
| TC | det () const throw (cvmexception) |
| Matrix determinant. | |
| basic_scmatrix & | low_up (const basic_scmatrix &m, tint *nPivots) throw (cvmexception) |
| Low-up (LU) factorization. | |
| basic_scmatrix | low_up (tint *nPivots) const throw (cvmexception) |
| Low-up (LU) factorization. | |
| TR | cond () const throw (cvmexception) |
| Condition number reciprocal. | |
| basic_scmatrix & | inv (const basic_scmatrix &m) throw (cvmexception) |
| Matrix inversion. | |
| basic_scmatrix & | exp (const basic_scmatrix &m, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Matrix exponent. | |
| basic_scmatrix & | polynom (const basic_scmatrix &m, const CVector &v) throw (cvmexception) |
| Matrix polynomial. | |
| basic_scmatrix | polynom (const CVector &v) const |
| Matrix polynomial. | |
| CVector | eig (basic_scmatrix &mEigVect, bool bRightVect=true) const throw (cvmexception) |
| Eigenvalues and eigenvectors. | |
| basic_scmatrix & | cholesky (const basic_schmatrix< TR, TC > &m) throw (cvmexception) |
| Cholesky factorization. | |
| basic_scmatrix & | bunch_kaufman (const basic_schmatrix< TR, TC > &m, tint *nPivots) throw (cvmexception) |
| Bunch-Kaufman factorization. | |
| void | qr (basic_scmatrix< TR, TC > &mQ, basic_scmatrix< TR, TC > &mR) const throw (cvmexception) |
| QR factorization. | |
| void | lq (basic_scmatrix< TR, TC > &mL, basic_scmatrix< TR, TC > &mQ) const throw (cvmexception) |
| LQ factorization. | |
| void | ql (basic_scmatrix< TR, TC > &mQ, basic_scmatrix< TR, TC > &mL) const throw (cvmexception) |
| QL factorization. | |
| void | rq (basic_scmatrix< TR, TC > &mR, basic_scmatrix< TR, TC > &mQ) const throw (cvmexception) |
| RQ factorization. | |
 Public Member Functions inherited from basic_cmatrix< TR, TC > Public Member Functions inherited from basic_cmatrix< TR, TC > | |
| basic_cmatrix () | |
| Default constructor. | |
| basic_cmatrix (tint nM, tint nN) | |
| Constructor. | |
| basic_cmatrix (TC *pd, tint nM, tint nN) | |
| Constructor. | |
| basic_cmatrix (const TC *pd, tint nM, tint nN) | |
| Constructor. | |
| basic_cmatrix (const basic_cmatrix &m) | |
| Copy constructor. | |
| basic_cmatrix (basic_cmatrix &&m) noexcept | |
| Move constructor. | |
| basic_cmatrix (const CVector &v, bool bBeColumn=true) | |
| Constructor. | |
| basic_cmatrix (const basic_rmatrix< TR > &m, bool bRealPart=true) | |
| Constructor. | |
| basic_cmatrix (const TR *pRe, const TR *pIm, tint nM, tint nN) | |
| Constructor. | |
| basic_cmatrix (const basic_rmatrix< TR > &mRe, const basic_rmatrix< TR > &mIm) | |
| Constructor. | |
| basic_cmatrix (basic_cmatrix &m, tint nRow, tint nCol, tint nHeight, tint nWidth) | |
| Submatrix constructor. | |
| CVector | diag (tint nDiag) throw (cvmexception) |
| Diagonal as l-value. | |
| basic_cmatrix & | operator= (const basic_cmatrix &m) throw (cvmexception) |
| Assignment operator. | |
| basic_cmatrix & | operator= (basic_cmatrix &&m) throw (cvmexception) |
| Move assignment operator. | |
| basic_cmatrix & | assign (tint nRow, tint nCol, const basic_cmatrix &m) throw (cvmexception) |
| Assignment to submatrix. | |
| basic_cmatrix & | assign_real (const basic_rmatrix< TR > &mRe) throw (cvmexception) |
| Assignment to real parts. | |
| basic_cmatrix & | assign_imag (const basic_rmatrix< TR > &mIm) throw (cvmexception) |
| Assignment to imaginary parts. | |
| basic_cmatrix & | resize (tint nNewM, tint nNewN) throw (cvmexception) |
| Changes dimensions. | |
| bool | operator== (const basic_cmatrix &m) const |
| Matrix comparison. | |
| bool | operator!= (const basic_cmatrix &m) const |
| Matrix comparison. | |
| basic_cmatrix & | operator<< (const basic_cmatrix &m) throw (cvmexception) |
| Matrix replacement. | |
| basic_cmatrix | operator+ (const basic_cmatrix &m) const throw (cvmexception) |
| Addition operator. | |
| basic_cmatrix | operator- (const basic_cmatrix &m) const throw (cvmexception) |
| Subtraction operator. | |
| basic_cmatrix & | sum (const basic_cmatrix &m1, const basic_cmatrix &m2) throw (cvmexception) |
| Sum of matrices. | |
| basic_cmatrix & | diff (const basic_cmatrix &m1, const basic_cmatrix &m2) throw (cvmexception) |
| Difference of matrices. | |
| basic_cmatrix & | operator+= (const basic_cmatrix &m) throw (cvmexception) |
| Increment operator. | |
| basic_cmatrix & | operator-= (const basic_cmatrix &m) throw (cvmexception) |
| Decrement operator. | |
| basic_cmatrix & | transpose (const basic_cmatrix &m) throw (cvmexception) |
| Matrix transposition. | |
| basic_cmatrix & | conj (const basic_cmatrix &m) throw (cvmexception) |
| Matrix conjugation. | |
| basic_cmatrix | operator* (const basic_cmatrix &m) const throw (cvmexception) |
| Matrix-matrix product. | |
| basic_cmatrix & | mult (const basic_cmatrix &m1, const basic_cmatrix &m2) throw (cvmexception) |
| Matrix-matrix product. | |
| basic_cmatrix & | rank1update_u (const CVector &vCol, const CVector &vRow) throw (cvmexception) |
| Rank-1 update (unconjugated) | |
| basic_cmatrix & | rank1update_c (const CVector &vCol, const CVector &vRow) throw (cvmexception) |
| Rank-1 update (conjugated) | |
| basic_cmatrix & | solve (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB, TR &dErr) throw (cvmexception) |
| Linear solver. | |
| basic_cmatrix & | solve_tran (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB, TR &dErr) throw (cvmexception) |
| Linear solver (transposed) | |
| basic_cmatrix & | solve_conj (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB, TR &dErr) throw (cvmexception) |
| Linear solver (conjugated) | |
| basic_cmatrix & | solve (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB) throw (cvmexception) |
| Linear solver. | |
| basic_cmatrix & | solve_tran (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB) throw (cvmexception) |
| Linear solver (transposed) | |
| basic_cmatrix & | solve_conj (const basic_scmatrix< TR, TC > &mA, const basic_cmatrix &mB) throw (cvmexception) |
| Linear solver (conjugated) | |
| basic_cmatrix & | solve_lu (const basic_scmatrix< TR, TC > &mA, const basic_scmatrix< TR, TC > &mLU, const tint *pPivots, const basic_cmatrix &mB, TR &dErr) throw (cvmexception) |
| LU factorization based linear solver. | |
| basic_cmatrix & | solve_lu (const basic_scmatrix< TR, TC > &mA, const basic_scmatrix< TR, TC > &mLU, const tint *pPivots, const basic_cmatrix &mB) throw (cvmexception) |
| LU factorization based linear solver. | |
| RVector | svd () const throw (cvmexception) |
| Singular value decomposition. | |
| RVector | svd (basic_scmatrix< TR, TC > &mU, basic_scmatrix< TR, TC > &mVH) const throw (cvmexception) |
| Singular value decomposition. | |
| basic_cmatrix | pinv (TR threshold=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Pseudo (generalized) inversion. | |
| basic_cmatrix & | pinv (const basic_cmatrix &mA, TR threshold=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Pseudo (generalized) inversion. | |
| basic_cmatrix | gels (bool conjugate, const basic_cmatrix &mB, basic_cvector< TR, TC > &vErr) const throw (cvmexception) |
| Overdetermined or underdetermined linear solver. | |
| basic_cmatrix & | gels (bool conjugate, const basic_cmatrix &mA, const basic_cmatrix &mB, basic_cvector< TR, TC > &vErr) throw (cvmexception) |
| Overdetermined or underdetermined linear solver. | |
| basic_cvector< TR, TC > | gels (bool conjugate, const basic_cvector< TR, TC > &vB, TC &dErr) const throw (cvmexception) |
| Overdetermined or underdetermined linear solver. | |
| basic_cmatrix | gelsy (const basic_cmatrix &mB, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| basic_cmatrix & | gelsy (const basic_cmatrix &mA, const basic_cmatrix &mB, tint &rank, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Linear least squares problem. | |
| basic_cvector< TR, TC > | gelsy (const basic_cvector< TR, TC > &vB, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| basic_cmatrix | gelss (const basic_cmatrix &mB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| basic_cmatrix & | gelss (const basic_cmatrix &mA, const basic_cmatrix &mB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Linear least squares problem. | |
| basic_cvector< TR, TC > | gelss (const basic_cvector< TR, TC > &vB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| basic_cmatrix | gelsd (const basic_cmatrix &mB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| basic_cmatrix & | gelsd (const basic_cmatrix &mA, const basic_cmatrix &mB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) throw (cvmexception) |
| Linear least squares problem. | |
| basic_cvector< TR, TC > | gelsd (const basic_cvector< TR, TC > &vB, basic_rvector< TR > &sv, tint &rank, TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Linear least squares problem. | |
| tint | rank (TR tol=basic_cvmMachSp< TR >()) const throw (cvmexception) |
| Matrix rank. | |
| void | qr (basic_cmatrix< TR, TC > &mQ, basic_scmatrix< TR, TC > &mR) const throw (cvmexception) |
| QR factorization ("economy" mode) | |
| void | qr (basic_scmatrix< TR, TC > &mQ, basic_cmatrix< TR, TC > &mR) const throw (cvmexception) |
| QR factorization ("full" mode) | |
| void | lq (basic_scmatrix< TR, TC > &mL, basic_cmatrix< TR, TC > &mQ) const throw (cvmexception) |
| LQ factorization ("economy" mode) | |
| void | lq (basic_cmatrix< TR, TC > &mL, basic_scmatrix< TR, TC > &mQ) const throw (cvmexception) |
| LQ factorization ("full" mode) | |
| void | rq (basic_scmatrix< TR, TC > &mR, basic_cmatrix< TR, TC > &mQ) const throw (cvmexception) |
| RQ factorization ("economy" mode) | |
| void | rq (basic_cmatrix< TR, TC > &mR, basic_scmatrix< TR, TC > &mQ) const throw (cvmexception) |
| RQ factorization ("full" mode) | |
| void | ql (basic_cmatrix< TR, TC > &mQ, basic_scmatrix< TR, TC > &mL) const throw (cvmexception) |
| QL factorization ("economy" mode) | |
| void | ql (basic_scmatrix< TR, TC > &mQ, basic_cmatrix< TR, TC > &mL) const throw (cvmexception) |
| QL factorization ("full" mode) | |
| basic_cmatrix & | geru (TC alpha, const CVector &vCol, const CVector &vRow) throw (cvmexception) |
| Rank-1 update matrix-vector operation (unconjugated) | |
| basic_cmatrix & | gerc (TC alpha, const CVector &vCol, const CVector &vRow) throw (cvmexception) |
| Rank-1 update matrix-vector operation (conjugated) | |
| basic_cmatrix & | gemm (const basic_cmatrix &m1, bool bConj1, const basic_cmatrix &m2, bool bConj2, TC cAlpha, TC cBeta) throw (cvmexception) |
| Generic matrix-matrix operation. | |
| basic_cmatrix & | hemm (bool bLeft, const basic_schmatrix< TR, TC > &ms, const basic_cmatrix &m, TC cAlpha, TC cBeta) throw (cvmexception) |
| Generic hermitian matrix-matrix operation. | |
| TR | norm2 () const override |
| 2-norm | |
 Public Member Functions inherited from Matrix< TR, TC > Public Member Functions inherited from Matrix< TR, TC > | |
| tint | msize () const |
| Number of rows. | |
| tint | nsize () const |
| Number of columns. | |
| tint | ld () const |
| Leading dimension. | |
| tint | rowofmax () const |
| Row with maximum element. | |
| tint | rowofmin () const |
| Row with minimum element. | |
| tint | colofmax () const |
| Column with maximum element. | |
| tint | colofmin () const |
| Column with minimum element. | |
| TR | norm1 () const override |
| 1-norm | |
 Public Member Functions inherited from basic_array< TR, TC > Public Member Functions inherited from basic_array< TR, TC > | |
| basic_array () | |
| Default constructor. | |
| basic_array (tint nSize, bool bZeroMemory=true) | |
| Constructor. | |
| basic_array (TC *pd, tint nSize, tint nIncr=1) | |
| Constructor. | |
| basic_array (const TC *pd, tint nSize, tint nIncr=1) | |
| Constructor. | |
| basic_array (const TC *begin, const TC *end) | |
| Constructor. | |
| basic_array (const basic_array &a) | |
| Copy constructor. | |
| basic_array (basic_array &&a) noexcept | |
| Move constructor. | |
| basic_array & | operator= (const basic_array &a) throw (cvmexception) |
| Assignment operator. | |
| basic_array & | operator= (basic_array &&a) throw (cvmexception) |
| Move assignment operator. | |
| virtual | ~basic_array () |
| Destructor. | |
| tint | size () const |
| Size (length) of array. | |
| TC * | get () |
| Pointer to data. | |
| const TC * | get () const |
| Const pointer to data. | |
| operator TC * () | |
| Type cast to pointer to data. | |
| operator const TC * () const | |
| Type cast to constant pointer to data. | |
| tint | incr () const |
| Increment between elements. | |
| tint | indofmax () const |
| Index of element with maximum module. | |
| tint | indofmin () const |
| Index of element with minimum module. | |
| virtual TR | norm () const |
| Euclidean norm. | |
| iterator | begin () |
| (STL) iterator to begin | |
| const_iterator | begin () const |
| (STL) const iterator to begin | |
| iterator | end () |
| (STL) iterator to end | |
| const_iterator | end () const |
| (STL) const iterator to end | |
| reverse_iterator | rbegin () |
| (STL) iterator to begin reversed | |
| const_reverse_iterator | rbegin () const |
| (STL) const iterator to begin reversed | |
| reverse_iterator | rend () |
| (STL) iterator to end reversed | |
| const_reverse_iterator | rend () const |
| (STL) const iterator to end reversed | |
| size_type | max_size () const |
| (STL) maximum possible size of array | |
| size_type | capacity () const |
| (STL) current capacity of array, equal to size() | |
| bool | empty () const |
| (STL) is array empty | |
| reference | front () |
| (STL) reference to first element | |
| const_reference | front () const |
| (STL) const reference to first element | |
| reference | back () |
| (STL) reference to last element | |
| const_reference | back () const |
| (STL) const reference to last element | |
| void | assign (size_type n, const TC &val) throw (cvmexception) |
| (STL) assigns given value to n-th element (0-based) | |
| void | assign (const_iterator begin, const_iterator end) throw (cvmexception) |
| (STL) assigns begin-end iteartor range to array | |
| void | clear () |
| (STL) clears array, dealocates memory and sets size() to zero | |
| void | swap (basic_array &v) throw (cvmexception) |
| (STL) swaps array values, throws cvmexception if sizes are different | |
| reference | at (size_type n) throw (cvmexception) |
| (STL) returns reference to n-th element of array (0-based), throws cvmexception if n is out of boundaries | |
| const_reference | at (size_type n) const throw (cvmexception) |
| (STL) returns const reference to n-th element of array (0-based), throws cvmexception if n is out of boundaries | |
| void | push_back (const TC &x) throw (cvmexception) |
| (STL) pushes new value to the end of array | |
| void | pop_back () throw (cvmexception) |
| (STL) removes last element from array | |
| iterator | insert (iterator position, const TC &x) throw (cvmexception) |
| (STL) inserts element to given position in array | |
| iterator | erase (iterator position) throw (cvmexception) |
| (STL) removes element from given position in array | |
Additional Inherited Members | |
 Public Types inherited from basic_array< TR, TC > Public Types inherited from basic_array< TR, TC > | |
| typedef TC | value_type |
| STL-specific value type definition. | |
| typedef value_type * | pointer |
| STL-specific value pointer definition. | |
| typedef value_type * | iterator |
| STL-specific iterator definition. | |
| typedef const value_type * | const_iterator |
| STL-specific const iterator definition. | |
| typedef const value_type * | const_pointer |
| STL-specific const pointer definition. | |
| typedef value_type & | reference |
| STL-specific reference definition. | |
| typedef const value_type & | const_reference |
| STL-specific const reference definition. | |
| typedef size_t | size_type |
| STL-specific size type definition. | |
| typedef ptrdiff_t | difference_type |
| STL-specific difference type definition. | |
| typedef std::reverse_iterator < const_iterator > | const_reverse_iterator |
| STL-specific const reverse iterator definition. | |
| typedef std::reverse_iterator < iterator > | reverse_iterator |
| STL-specific reverse iterator definition. | |
 Protected Member Functions inherited from Matrix< TR, TC > Protected Member Functions inherited from Matrix< TR, TC > | |
| Matrix () | |
| Default constructor. | |
| Matrix (tint nM, tint nN, tint nLD, bool bZeroMemory) | |
| Constructor. | |
| Matrix (TC *pd, tint nM, tint nN, tint nLD, tint nSize) | |
| Constructor. | |
| Matrix (const TC *pd, tint nM, tint nN, tint nLD, tint nSize) | |
| Constructor. | |
| Matrix (const BaseArray &v, bool bBeColumn) | |
| Constructor. | |
| Matrix (Matrix &&m) noexcept | |
| Move constructor. | |
| Matrix & | operator= (Matrix &&m) throw (cvmexception) |
| Move assignment operator. | |
 Protected Member Functions inherited from SqMatrix< TR, TC > Protected Member Functions inherited from SqMatrix< TR, TC > | |
| SqMatrix () | |
| internal constructor | |
| virtual | ~SqMatrix () |
 Protected Attributes inherited from Matrix< TR, TC > Protected Attributes inherited from Matrix< TR, TC > | |
| tint | mm |
| Number of rows. | |
| tint | mn |
| Number of columns. | |
| tint | mld |
| Leading dimension. | |
End-user class encapsulating hermitian matrix of complex numbers.
TR type stands for treal, TC type stands for tcomplex. Please use predefined schmatrix class in your applications.
|
inline |
Default constructor.
Creates empty hermitian matrix. No memory gets allocated.
|
inlineexplicit |
Constructor.
Creates 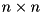 schmatrix object where
schmatrix object where 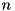 is passed in
is passed in nDim parameter. Constructor sets all elements to zero. It throws cvmexception in case of non-positive size passed or memory allocation failure. Example:
prints
| [in] | nDim | Number of rows and columns. |
|
inline |
Constructor.
Creates 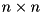 schmatrix object where
schmatrix object where 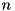 is passed in
is passed in nDim parameter. It throws cvmexception in case of non-positive size passed or if the matrix created doesn't appear to be hermitian. Hermiticity tolerance is set by parameter tol. Unlike others, this constructor does not allocate memory. It just shares memory with array pointed to by pd (for matrices nIncr=1 is always satisfied). If subsequent application flow would change the array passed so it becomes not hermitian matrix anymore then results are not predictable.
| [in] | pd | Pointer to array to share memory with. |
| [in] | nDim | Number of rows and columns. |
| [in] | tol | Hermiticity tolerance. |
|
inline |
Constructor.
Creates 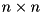 schmatrix object where
schmatrix object where 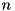 is passed in
is passed in nDim parameter. Constructor throws cvmexception in case of non-positive sizes passed or if the matrix created doesn't appear to be hermitian. Hermiticity tolerance is set by parameter tol. This is const version, it allocates memory and copies every element (deep copy) from external array pointed to by pd parameter. It copies nDim*nDim elements total.
| [in] | pd | Const pointer to external array. |
| [in] | nDim | Number of rows and columns. |
| [in] | tol | Hermiticity tolerance. |
|
inline |
Copy constructor.
Creates schmatrix object as a copy of hermitian matrix m. It throws cvmexception in case of memory allocation failure.
| [in] | m | schmatrix to copy from. |
|
inline |
Move constructor.
Implements move semantics introduced in new C++ standard. Moves data ownership from other matrix to newly created object. It's usually executed implicitly in cases like this:
or this
Here temporary result of calling b.operator+(c) will not be destroyed but rather moved to newly created object a.
| [in] | m | rvalue reference to other matrix. |
|
inlineexplicit |
Constructor.
Creates schmatrix object as a copy of complex matrix m. It's assumed that  matrix
matrix m must have equal sizes, i.e.  is satisfied, and must be hermitian. Hermiticity tolerance is set by parameter
is satisfied, and must be hermitian. Hermiticity tolerance is set by parameter tol. Constructor throws cvmexception if this is not true or in case of memory allocation failure.
| [in] | m | cmatrix to copy from. |
| [in] | tol | Hermiticity tolerance. |
Definition at line 34473 of file cvm.h.

|
inlineexplicit |
Constructor.
Creates schmatrix object of size v.size() by v.size() and assigns real vector v to its main diagonal. Constructor throws cvmexception in case of memory allocation failure.
| [in] | v | rvector to copy main diagonal from. |
Definition at line 34507 of file cvm.h.

|
inlineexplicit |
Constructor.
Creates schmatrix object having the same dimension as real symmetric matrix m and copies matrix m to its real part.
| [in] | m | srsmatrix to copy from. |
Definition at line 34534 of file cvm.h.

|
inline |
Constructor.
Creates schmatrix object of dimension nDim and copies every element of arrays pointed to by pRe and pIm to real and imaginary part of the matrix created respectively. Use nullptr pointer to fill up appropriate part with zero values. Contructor checks that the matrix is hermitian and throws cvmexception otherwise. Hermiticity tolerance is set by parameter tol. Constructor also throws cvmexception in case of memory allocation failure.
|
inline |
Constructor.
Creates schmatrix object of dimension mRe.msize() (if it differs from mIm.msize() then constructor throws cvmexception) and copies matrices mRe and mIm to real and imaginary part of the matrix created respectively. Contructor checks that the matrix is hermitian and throws cvmexception otherwise. Hermiticity tolerance is set by parameter tol. Constructor also throws cvmexception in case of memory allocation failure.
|
inline |
Submatrix constructor.
Creates schmatrix object as submatrix of hermitian matrix m. It means that the object created shares memory with some part of m. This part is defined by its upper left corner (parameter nRowCol, CVM0 based) and its dimension (parameter nDim).
|
inline |
Value of element (not l-value)
Operator returns value of a particular element of calling matrix by its row and column index. Indexes passed are CVM0 based. Operator throws cvmexception if nRow or nCol is outside of boundaries.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 34641 of file cvm.h.

|
inline |
Column as not l-value.
Operator creates cvector object as a copy of nCol-th column (CVM0 based) of calling matrix. Operator throws cvmexception if nCol is outside of boundaries.
| [in] | nCol | Index of column (CVM0 based). |
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 34649 of file cvm.h.

|
inline |
Row as not l-value.
Operator creates cvector object as a copy of nRow-th row (CVM0 based) of calling matrix. Operator throws cvmexception if nRow is outside of boundaries.
| [in] | nRow | Index of row (CVM0 based). |
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 34656 of file cvm.h.

|
inline |
Diagonal (not l-value)
Operator creates cvector object as a copy of nDiag-th diagonal of calling matrix where nDiag=0 for main diagonal, nDiag<0 for lower diagonals and nDiag>0 for upper ones. Operator throws cvmexception if nDiag is outside of boundaries.
| [in] | nDiag | Index of diagonal (0 for main diagonal, negative for lower, positive for upper one). |
Reimplemented from basic_cmatrix< TR, TC >.
|
inline |
Real part (not l-value)
Creates object of type const rmatrix as real part of calling matrix. Please note that, unlike cvector::real(), this function creates new object not sharing memory with real part of calling matrix, i.e. the matrix returned is not l-value.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 34669 of file cvm.h.

|
inline |
Imaginary part (not l-value)
Creates object of type const rmatrix as imaginary part of calling matrix. Please note that, unlike cvector::imag(), this function creates new object not sharing memory with imaginary part of calling matrix, i.e. the matrix returned is not l-value.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 34677 of file cvm.h.

|
inline |
Assignment operator.
Sets every element of calling schmatrix to be equal to appropriate element of hermitian matrix m and returns reference to the matrix changed. Operator throws cvmexception in case of different matrix dimensions.
| [in] | m | schmatrix to assign from. |
Definition at line 34716 of file cvm.h.

|
inline |
Move assignment operator.
Implements move semantics introduced in new C++ standard. Moves data ownership from other matrix to calling object. It's usually executed implicitly in cases like this:
Here temporary result of calling b.operator+(c) will not be destroyed but rather moved to calling object a.
| [in] | m | rvalue reference to other matrix. |
Definition at line 34736 of file cvm.h.

|
inline |
Vector (as array) assignment.
Sets every element of calling hermitian matrix to be equal to appropriate element of rvector v as an array. Assignment is performed according to matrix storage (by columns). It's assumed that vector passed is long enough to fill calling matrix. Function throws cvmexception otherwise. Function also throws cvmexception if the matrix changed doesn't appear to be hermitian. Hermiticity tolerance is set by parameter tol.
| [in] | v | cvector to assign. |
| [in] | tol | Hermiticity tolerance. |
Definition at line 34771 of file cvm.h.
|
inline |
External array assignment.
Sets every element of calling hermitian matrix to be equal to appropriate element of array pointed to by parameter pd and returns reference to the matrix changed. Assignment is performed according to matrix storage (by columns). It's assumed that array passed is long enough to fill calling matrix. Function throws cvmexception if the matrix changed doesn't appear to be hermitian. Hermiticity tolerance is set by parameter tol.
| [in] | pd | Const pointer to external array. |
| [in] | tol | Hermiticity tolerance. |
|
inline |
Assignment to submatrix.
Sets main submatrix of calling hermitian matrix beginning with row and column nRowCol to hermitian matrix m and returns reference to the matrix changed. Function throws cvmexception if nRowCol is not positive or matrix m doesn't fit. Indexes are CVM0 based.
| [in] | nRowCol | Row and column index (CVM0 based). |
| [in] | m | Reference to hermitian matrix to assign. |
Definition at line 34846 of file cvm.h.

|
inline |
Sets both elements to keep matrix hermitian.
Sets main submatrix of calling hermitian matrix beginning with row and column nRowCol to hermitian matrix m and returns reference to the matrix changed. Function throws cvmexception if nRowCol is out of boundaries (it's CVM0 based).
| [in] | nRow | Row (and column) index to set (CVM0 based). |
| [in] | nCol | Column (and row) index to set (CVM0 based). |
| [in] | c | Element value to set to. |
|
inline |
Sets lower and upper diagonals.
Assigns complex vector vDiag to 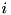 -th diagonal of calling hermitian matrix (
-th diagonal of calling hermitian matrix ( 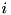 is passed in
is passed in nDiag parameter), where 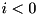 for lower diagonals and
for lower diagonals and 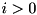 for upper ones. Function also assigns conjugated vector to
for upper ones. Function also assigns conjugated vector to 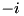 -th diagonal (thus calling matrix remains hermitian). Function returns reference to the matrix changed. Function throws cvmexception if parameter
-th diagonal (thus calling matrix remains hermitian). Function returns reference to the matrix changed. Function throws cvmexception if parameter nDiag is equal to zero (use set_main_diag() instead), is outside of boundaries or if vector vDiag passed has size not equal to msize()-abs(nDiag).
| [in] | nDiag | Diagonal index to set. |
| [in] | vDiag | cvector to set diagonal(s) to. |
Definition at line 34922 of file cvm.h.
|
inline |
Sets main diagonal.
Assigns real vector vDiag to main diagonal of calling hermitian matrix. Function returns reference to the matrix changed. Function throws cvmexception if vector vDiag passed has size not equal to msize().
| [in] | vDiag | rvector to set main diagonal to. |
Definition at line 34965 of file cvm.h.

|
inline |
Assigns real symmetric matrix to real part.
Sets real part of calling hermitian matrix to be equal to real symmetric matrix mRe. Function returns reference to the matrix changed. It throws cvmexception in case of different sizes of the operands.
| [in] | mRe | srsmatrix to assign to real part. |
Definition at line 34998 of file cvm.h.

|
inline |
Sets all real parts to one value.
Sets real part of every element of calling matrix to be equal to parameter d and returns reference to the matrix changed.
| [in] | d | Value to set to. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Changes dimension.
Changes dimension of calling square matrix to nNewDim and returns reference to the matrix changed. In case of increasing of its size, the matrix is filled up with zeroes. Function throws cvmexception in case of negative dimension passed or memory allocation failure.
| [in] | nNewDim | New dimension. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Matrix comparison.
Operator compares calling hermitian matrix with hermitian matrix m and returns true if they have same dimensions and their appropriate elements differ by not more than cvmMachMin() (the smallest normalized positive number). Returns false otherwise.
| [in] | m | hermitian matrix to compare to. |
Definition at line 35045 of file cvm.h.

|
inline |
Matrix comparison.
Operator compares calling hermitian matrix with hermitian matrix m and returns true if they have different sizes or at least one of their appropriate elements differs by more than cvmMachMin() (the smallest normalized positive number). Returns false otherwise.
| [in] | m | srsmatrix to compare to. |
|
inline |
Matrix replacement.
Destroys calling hermitian matrix, creates a new one as a copy of hermitian matrix m and returns reference to the matrix changed. Operator throws cvmexception in case of memory allocation failure.
| [in] | m | schmatrix to replace by. |
|
inline |
Addition operator.
Creates object of type schmatrix as sum of calling hermitian matrix and hermitian matrix m. Operator throws cvmexception in case of different sizes of the operands or memory allocation failure.
| [in] | m | schmatrix to add to calling one. |
Definition at line 35150 of file cvm.h.

|
inline |
Subtraction operator.
Creates object of type schmatrix as difference of calling hermitian matrix and hermitian matrix m. It throws cvmexception in case of different sizes of the operands or memory allocation failure.
| [in] | m | schmatrix to subtract from calling one. |
Definition at line 35186 of file cvm.h.

|
inline |
Sum of matrices.
Assigns sum of hermitian matrices m1 and m2 to calling hermitian matrix and returns reference to the matrices changed. It throws cvmexception in case of different sizes of the operands.
Definition at line 35223 of file cvm.h.

|
inline |
Difference of matrices.
Assigns difference of hermitian matrices m1 and m2 to calling hermitian matrix and returns reference to the matrix changed. It throws cvmexception in case of different sizes of the operands.
Definition at line 35260 of file cvm.h.

|
inline |
Increment operator.
Adds schmatrix m to calling hermitian matrix and returns reference to the matrix changed. It throws cvmexception in case of different sizes of the operands.
| [in] | m | schmatrix to increment by. |
Definition at line 35303 of file cvm.h.

|
inline |
Decrement operator.
Subtracts schmatrix m from calling hermitian matrix and returns reference to the matrix changed. It throws cvmexception in case of different sizes of the operands.
| [in] | m | schmatrix to decrement by. |
Definition at line 35345 of file cvm.h.

|
inline |
Unary minus operator.
Creates object of type scmatrix as calling matrix multiplied by -1. It throws cvmexception in case of memory allocation failure.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Plus identity, prefix.
Adds identity matrix to calling square complex matrix and returns reference to the matrix changed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Plus identity, postfix.
Adds identity matrix to calling square complex matrix and returns reference to the matrix changed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Minus identity, prefix.
Subtracts identity matrix from calling square complex matrix and returns reference to the matrix changed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Minus identity, postfix.
Subtracts identity matrix from calling square complex matrix and returns reference to the matrix changed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Multiply by real number operator.
Creates object of type scmatrix as product of calling matrix and real number dMult. It throws cvmexception in case of memory allocation failure.
| [in] | dMult | Number to multiply by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Divide by real number operator.
Creates object of type scmatrix as quotient of calling matrix and real number dDiv. It throws cvmexception if dDiv has absolute value equal or less than cvmMachMin() (the smallest normalized positive number). It also throws exception in case of memory allocation failure.
| [in] | dDiv | Number to divide by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Multiply by complex number operator.
Creates object of type scmatrix as product of calling matrix and complex number cMult. It throws cvmexception in case of memory allocation failure.
| [in] | cMult | Number to multiply by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Divide by complex number operator.
Creates object of type scmatrix as quotient of calling matrix and complex number cDiv. It throws cvmexception if cDiv has absolute value equal or less than cvmMachMin() (the smallest normalized positive number). It also throws exception in case of memory allocation failure.
| [in] | cDiv | Number to divide by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Multiply by real number and assign.
Multiplies calling square complex matrix by real number dMult and returns reference to the matrix changed.
| [in] | dMult | Number to multiply by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Divide by real number and assign.
Divides calling square complex matrix by real number dDiv and returns reference to the matrix changed. It throws cvmexception if dDiv has absolute value equal or less than cvmMachMin() (the smallest normalized positive number).
| [in] | dDiv | Number to divide by. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Matrix normalizer.
Normalizes calling matrix so its Euclidean norm() becomes equal to 1 if it was greater than cvmMachMin() (the smallest normalized positive number) before the call. Does nothing otherwise.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Matrix transposition.
Creates object of type schmatrix as transposed calling hermitian matrix.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 35473 of file cvm.h.

|
inline |
Does nothing and returns copy of calling hermitian matrix.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Matrix transposition.
Sets calling hermitian matrix to be equal to hermitian matrix m transposed. Function throws cvmexception in case of not appropriate sizes of the operands.
| [in] | m | schmatrix to transpose. |
Definition at line 35525 of file cvm.h.

|
inline |
|
inline |
Matrix transposition (in-place)
Makes calling hermitian matrix to be equal to transposed itself. Function throws cvmexception in case of memory allocation failure.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Does nothing and returns reference to calling symmetric matrix.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Matrix-vector product.
Creates object of type cvector as product of calling matrix and vector v. Function throws cvmexception if the number of columns of the calling matrix differs from size of the vector v. Use basic_cvector::mult(const basic_cmatrix<TR,TC>&,const basic_cvector<TR,TC>&) to avoid new object creation.
| [in] | v | cvector to compute product with. |
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 35592 of file cvm.h.

|
inline |
Matrix-matrix product.
Creates object of type cmatrix as product of calling square complex matrix and matrix m. Operator throws cvmexception if number of columns of calling matrix differs from number of rows of the matrix m. Use mult() to avoid new object creation.
| [in] | m | cmatrix to compute product with. |
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 35601 of file cvm.h.

|
inline |
Matrix-matrix product.
Creates object of type scmatrix as product of calling hermitian matrix and square complex matrix m. Operator throws cvmexception if dimension of calling matrix differs from dimension the matrix m. Use mult() to avoid new object creation.
| [in] | m | scmatrix to compute product with. |
Definition at line 35643 of file cvm.h.
|
inline |
Linear solver operator.
Creates cvector object as solution 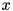 of linear equation
of linear equation 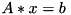 where calling matrix is square complex matrix
where calling matrix is square complex matrix  and parameter
and parameter vB is vector  . Operator throws cvmexception in case of inappropriate sizes of the operands or when matrix
. Operator throws cvmexception in case of inappropriate sizes of the operands or when matrix  is close to singular.
is close to singular.
| [in] | vB | cvector  . . |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Rank-1 update matrix-vector operation.
Calls one of ZHERK routines of the BLAS library performing rank-1 update matrix-vector operation defined as
![\[ A=\alpha\,\begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} \begin{pmatrix} v_1^* & v_2^* & \cdots & v_n^* \end{pmatrix} + \beta A, \]](form_144.png)
where 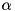 and
and 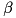 are real numbers (parameters
are real numbers (parameters alpha and beta),  is calling hermitian matrix and
is calling hermitian matrix and 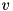 is complex vector (parameter
is complex vector (parameter v). Function returns reference to the matrix changed and throws cvmexception in case of inappropriate sizes of the operands.
| [in] | alpha | Multiplier 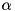 . . |
| [in] | v | cvector 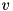 . . |
| [in] | beta | Multiplier 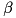 . . |
Definition at line 35707 of file cvm.h.

|
inline |
Rank-1 update matrix-matrix operation.
Calls ZHERK routine of the BLAS library performing rank-1 update matrix-vector operation defined as
![\[ A=\alpha MM^H + \beta A\quad\text{or}\quad A=\alpha M^HM + \beta A. \]](form_145.png)
where 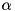 and
and 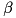 are real numbers (parameters
are real numbers (parameters alpha and beta),  is calling hermitian matrix and
is calling hermitian matrix and  is complex matrix (parameter
is complex matrix (parameter m). First operation is performed if bTransp passed is false and second one otherwise. Function returns reference to the matrix changed and throws cvmexception in case of inappropriate sizes of the operands.
| [in] | bTransp | Use transposed operation. |
| [in] | alpha | Multiplier 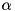 . . |
| [in] | m | cmatrix  . . |
| [in] | beta | Multiplier 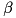 . . |
Definition at line 35781 of file cvm.h.

|
inline |
Rank-1 update matrix-vector operation.
Calls ZHER2K routine of the BLAS library performing rank-1 update matrix-vector operation defined as
![\[ A=\alpha v_1 v_2^* + \alpha^* v_2 v_1^* + \beta A, \]](form_146.png)
where 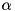 is complex and
is complex and 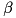 is real number (parameters
is real number (parameters alpha and beta),  is calling hermitian matrix and
is calling hermitian matrix and 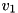 and
and  are complex vectors (parameters
are complex vectors (parameters v1 and v2). Function returns reference to the matrix changed and throws cvmexception in case of inappropriate sizes of the operands.
Definition at line 35836 of file cvm.h.

|
inline |
Rank-1 update matrix-matrix operation.
Calls ZHE2K routine of the BLAS library performing rank-1 update matrix-matrix operation defined as
![\[ A=\alpha M_1 M_2^H + \alpha^* M_2 M_1^H + \beta A\quad \text{or}\quad A=\alpha M_1^H M_2 + \alpha^* M_2^H M_1 + \beta A. \]](form_147.png)
where 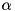 is complex and
is complex and 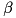 is real number (parameters
is real number (parameters alpha and beta),  is calling hermitian matrix and
is calling hermitian matrix and 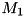 and
and 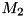 are complex matrices (parameters
are complex matrices (parameters m1 and m2). First operation is performed if bTransp passed is false and second one otherwise. Function returns reference to the matrix changed and throws cvmexception in case of inappropriate sizes of the operands.
| [in] | bTransp | Use transposed version of the operation. |
| [in] | alpha | Complex multiplier 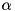 . . |
| [in] | m1 | cmatrix 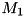 . . |
| [in] | m2 | cmatrix 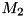 . . |
| [in] | beta | Real multiplier 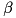 . . |
Definition at line 35925 of file cvm.h.

|
inline |
Matrix inversion.
This version sets calling matrix to be equal to hermitian matrix m inverted. Function throws cvmexception in case of inappropriate sizes of the operands or when the matrix to be inverted is close to singular.
| [in] | m | schmatrix to invert. |
|
inline |
Matrix inversion.
This version creates schmatrix object equal to calling hermitian matrix inverted. Function throws cvmexception in case of memory allocation failure or when the matrix to be inverted is close to singular.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 36009 of file cvm.h.

|
inline |
Matrix exponent.
Computes exponent of hermitian matrix using Pade approximation defined as
![\[ R_{pq}(z)=D_{pq}(z)^{-1}N_{pq}(z)=1+z+\dots+z^p/p!\,, \]](form_108.png)
where
![\[\begin{aligned} N_{pq}(z)&=\sum_{k=0}^p\frac{(p+q-k)!p!}{(p+q)!k!(q-k)!}z^k,\\ D_{pq}(z)&=\sum_{k=0}^q\frac{(p+q-k)!p!}{(p+q)!k!(q-k)!}(-z)^k \end{aligned}\]](form_109.png)
along with the matrix normalizing as described in Gene H. Golub, Charles F. Van Loan. Matrix Computations, The Johns Hopkins University Press, 1996, 694~p., ISBN 0-8018-5413-X, p. 572. Function uses DMEXP (or SMEXP for float version) FORTRAN subroutine implementing the algorithm. This version sets calling matrix to be equal to exponent of hermitian matrix m and returns reference to the matrix changed. The algorithm uses parameter tol as 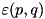 in order to choose constants
in order to choose constants 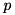 and
and 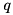 so that
so that
![\[ \varepsilon(p,q)\ge 2^{3-(p+q)}\frac{p!q!}{(p+q)!(p+q+1)!}. \]](form_113.png)
This parameter is equal to the largest relative spacing (see cvmMachSp() ) by default. Function throws cvmexception in case of inappropriate sizes of the operands or when LAPACK subroutine fails.
| [in] | m | schmatrix to compute exponent for. |
| [in] | tol | Computation tolerance. |
|
inline |
Matrix exponent.
Computes exponent of hermitian matrix using Pade approximation defined as
![\[ R_{pq}(z)=D_{pq}(z)^{-1}N_{pq}(z)=1+z+\dots+z^p/p!\,, \]](form_108.png)
where
![\[\begin{aligned} N_{pq}(z)&=\sum_{k=0}^p\frac{(p+q-k)!p!}{(p+q)!k!(q-k)!}z^k,\\ D_{pq}(z)&=\sum_{k=0}^q\frac{(p+q-k)!p!}{(p+q)!k!(q-k)!}(-z)^k \end{aligned}\]](form_109.png)
along with the matrix normalizing as described in Gene H. Golub, Charles F. Van Loan. Matrix Computations, The Johns Hopkins University Press, 1996, 694~p., ISBN 0-8018-5413-X, p. 572. Function uses DMEXP (or SMEXP for float version) FORTRAN subroutine implementing the algorithm. This version creates object of type schmatrix as exponent of calling hermitian matrix. The algorithm uses parameter tol as 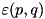 in order to choose constants
in order to choose constants 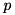 and
and 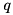 so that
so that
![\[ \varepsilon(p,q)\ge 2^{3-(p+q)}\frac{p!q!}{(p+q)!(p+q+1)!}. \]](form_113.png)
This parameter is equal to the largest relative spacing (see cvmMachSp() ) by default. Function throws cvmexception in case of inappropriate sizes of the operands or when LAPACK subroutine fails.
| [in] | tol | Computation tolerance. |
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 36187 of file cvm.h.

|
inline |
Matrix polynomial.
Computes hermitian matrix polynomial defined as
![\[ p(A)=b_0I+b_1A+\dots+b_qA^q \]](form_114.png)
using the Horner's rule:
![\[ \newcommand{\floor}{\operatorname{floor}}p(A)=\sum_{k=0}^r B_k(A^s)^k,\quad s=\floor(\!\sqrt{q}\,),\ r=\floor(q/s) \]](form_115.png)
where
![\[ B_k=\begin{cases} \sum\limits_{i=0}^{s-1}b_{sk+i} A^i, & k=0,1,\dots,r-1\\ \sum\limits_{i=0}^{q-sr}b_{sr+i} A^i, & k=r. \end{cases} \]](form_116.png)
See also Gene H. Golub, Charles F. Van Loan. Matrix Computations, The Johns Hopkins University Press, 1996, 694~p., ISBN 0-8018-5413-X, p. 568. Real coefficients 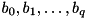 are passed in parameter
are passed in parameter v, where 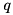 is equal to
is equal to v.size()-1, so the function computes matrix polynomial equal to
![\[ \mathtt{v[1]*I + v[2]*m +\cdots + v[v.size()]*m^{v.size()-1}} \]](form_118.png)
This version sets calling matrix to be equal to the polynomial of hermitian matrix m. Function uses ZPOLY (or CPOLY for float version) FORTRAN subroutine implementing the Horner's algorithm. Function throws cvmexception in case of inappropriate sizes of the operands.
| [in] | m | schmatrix to compute polynomial for. |
| [in] | v | Real vector of coefficients. |
Definition at line 36284 of file cvm.h.

|
inline |
Matrix polynomial.
Computes hemitian matrix polynomial defined as
![\[ p(A)=b_0I+b_1A+\dots+b_qA^q \]](form_114.png)
using the Horner's rule:
![\[ \newcommand{\floor}{\operatorname{floor}}p(A)=\sum_{k=0}^r B_k(A^s)^k,\quad s=\floor(\!\sqrt{q}\,),\ r=\floor(q/s) \]](form_115.png)
where
![\[ B_k=\begin{cases} \sum\limits_{i=0}^{s-1}b_{sk+i} A^i, & k=0,1,\dots,r-1\\ \sum\limits_{i=0}^{q-sr}b_{sr+i} A^i, & k=r. \end{cases} \]](form_116.png)
See also Gene H. Golub, Charles F. Van Loan. Matrix Computations, The Johns Hopkins University Press, 1996, 694~p., ISBN 0-8018-5413-X, p. 568. The coefficients 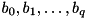 are passed in parameter
are passed in parameter v, where 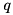 is equal to
is equal to v.size()-1, so the function computes matrix polynomial equal to
![\[ \mathtt{v[1]*I + v[2]*m +\cdots + v[v.size()]*m^{v.size()-1}} \]](form_118.png)
This version creates object of type schmatrix as the polynomial of hemitian symmetric matrix. Function uses ZPOLY (or CPOLY for float version) FORTRAN subroutine implementing the Horner's algorithm. Function throws cvmexception in case of memory allocation failure.
| [in] | v | Real vector of coefficients. |
Definition at line 36380 of file cvm.h.

|
inline |
Eigenvalues and eigenvectors.
Solves symmetric eigenvalue problem and creates rvector object equal to eigenvalues of calling hermitian matrix. The symmetric eigenvalue problem is defined as follows: given symmetric (hermitian) matrix  , find the eigenvalues
, find the eigenvalues  and the corresponding eigenvectors
and the corresponding eigenvectors 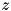 that satisfy the equation
that satisfy the equation
![\[ Az = \lambda z. \]](form_58.png)
Eigenvalues of hermitian complex matrix  are real and eigenvectors are complex. Function sets output parameter
are real and eigenvectors are complex. Function sets output parameter mEigVect to be equal to square matrix containing eigenvectors as columns. Function throws cvmexception in case of inappropriate calling object sizes or in case of convergence error.
| [out] | mEigVect | Eigenvectors of calling symmetric matrix. |
Definition at line 36441 of file cvm.h.

|
inline |
Eigenvalues.
Solves symmetric eigenvalue problem and creates rvector object equal to eigenvalues of calling hermitian matrix. The symmetric eigenvalue problem is defined as follows: given symmetric (hermitian) matrix  , find the eigenvalues
, find the eigenvalues  and the corresponding eigenvectors
and the corresponding eigenvectors 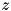 that satisfy the equation
that satisfy the equation
![\[ Az = \lambda z. \]](form_58.png)
Eigenvalues of hermitian complex matrix  are real. Function throws cvmexception in case of memory allocation failure or convergence error.
are real. Function throws cvmexception in case of memory allocation failure or convergence error.
Reimplemented from basic_scmatrix< TR, TC >.
Definition at line 36480 of file cvm.h.

|
inline |
Cholesky factorization.
Forms the Cholesky factorization of hermitian positive-definite calling matrix  defined as
defined as
![\[ A=U^H U, \]](form_148.png)
where 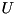 is upper triangular matrix. It utilizes one of
is upper triangular matrix. It utilizes one of ZPOTRF routines of the LAPACK library. Function creates scmatrix object equal to the factorization. Function throws cvmexception in case of convergence error.
|
inline |
Bunch-Kaufman factorization.
Forms the Bunch-Kaufman factorization of hermitian calling matrix (cited from the MKL library documentation):
![\[ A=PUDU^HP^H, \]](form_149.png)
where  is calling hermitian matrix,
is calling hermitian matrix, 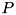 is a permutation matrix,
is a permutation matrix, 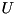 and
and 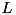 are upper and lower triangular matrices with unit diagonal, and
are upper and lower triangular matrices with unit diagonal, and 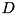 is a hermitian block-diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks.
is a hermitian block-diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks. 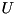 and
and 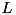 have 2-by-2 unit diagonal blocks corresponding to the 2-by-2 blocks of
have 2-by-2 unit diagonal blocks corresponding to the 2-by-2 blocks of 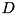 . It utilizes one of
. It utilizes one of ZHETRF routines of the LAPACK library. Function creates scmatrix object equal to the factorization of hermitian calling matrix. Function throws cvmexception in case of convergence error. Function is mostly designed to be used for subsequent calls of ZHETRS, ZHECON and ZHETRI routines of the LAPACK library. Currently it's used internally in det() flow when argument is symmetric but not positive-definite.
| [out] | nPivots | Pivot indices array. |
|
inline |
Identity matrix.
Sets calling square complex matrix to be equal to identity matrix and returns reference to the matrix changed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Set matrix to zero.
Sets every element of calling square complex matrix to be equal to zero and returns reference to the matrix changed. This function is faster than, for example, set(TR) with zero parameter passed.
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Randomizer (real part)
Fills real part of calling complex matrix with pseudo-random numbers distributed between dFrom and dTo. It returns reference to the matrix changed.
| [in] | dFrom | First limit. |
| [in] | dTo | Second limit. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inline |
Randomizer (imaginary part)
Fills imaginary part of calling complex matrix with pseudo-random numbers distributed between dFrom and dTo. It returns reference to the matrix changed.
| [in] | dFrom | First limit. |
| [in] | dTo | Second limit. |
Reimplemented from basic_scmatrix< TR, TC >.
|
inlineoverridevirtual |
Infinity norm.
Infinity norm of calling array that for vectors is defined as
![\[ {\|x\|}_\infty=\max_{i=1,\dots,n} |x_i| \]](form_16.png)
and for matrices as
![\[ {\|A\|}_\infty=\max_{i=1,\dots,m} \sum_{j=1}^{n} |a_{ij}|, \]](form_17.png)
Reimplemented from Matrix< TR, TC >.
Definition at line 36599 of file cvm.h.

|
inline |
|
inline |
|
inline |
 1.8.1.2
1.8.1.2