Introduction

[next] [tail] [up]

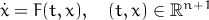
Runge is an Interactive Solver for Systems of Ordinary Differential Equations. It solves initial value problem (aka Cauchy problem) defined as the following: for a given system of ordinary differential equations

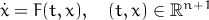
˙x = F(t,x), (t,x) ∈ ℝn+ 1

and given initial values

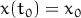
x(t0)= x0

find solution

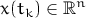
x(tk)∈ ℝn

at a given point of “time” i.e. for a given value 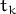$tk$ of independent variabl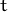e $t$ . Actually Runge produces solutions set

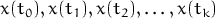
x(t0),x(t1),x(t2),..., x(tk)

where 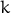$k$ is the number of steps taken. This allows to build trajectories of solutions.

1.2 Why Runge?

It’s fast. It utilizes BLAS and LAPACK FORTRAN libraries optimized for modern multi-core processors.
It’s interactive. It allows you to start a solution by mouse click on a plane.
It’s precise. It uses Runge Rule to adjust step length to satisfy required precision on each step.
It’s effective. When it needs to compute derivatives (Jacobian matrix, for example) it does that analytically, i.e. without using numerical methods.
It’s portable. It works on Windows and Linux (32 and 64 bit versions) and Mac OSX (64 bit only).
It’s open. It allows you to implement and embed your own algorithms (aka “solvers”).
It’s easy to use. It allows to export results to MS Excel and MATLAB.
It’s free. It’s distributed under Boost Software License.

1.3 System Types and Solvers

Runge comes with pre-installed solvers optimized for solving differential equations of different types:

Type 1. Generic non-autonomous system $x˙= F(t,x)$
Type 2. Generic autonomous system (it’s a subset of Type 1, i.e. you can use both types 1 and 2 for autonomous sytems — sometimes it makes sense for choosing appropriate solver) $x˙= F(x)$
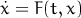
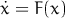
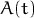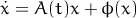
Type 3. Pseudo-linear system (here it’s assumed that $ϕ(x)$ is relatively small compared to matrix $A(t)$ ) $˙x = A(t)x + ϕ(x)$
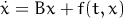
Type 4. Pseudo-linear system with constant matrix B $˙x = Bx + f(t,x)$

The solvers (algorithms) coming in standard package are:

Runge-Kutta process modification developed by R. England. Fast and precise method of fifth order suitable for solving systems of Type 1. See [1].
Exponential method modification developed by J.D. Lawson. It’s recommended for linear and quasi-linear systems of Type 1,3 and 4 (including stiff ones). The method is A-stable for linear systems, i.e. residuals do not depend on step length. See [2].
Implicit process developed by H.H. Rosenbrock. It’s recommended for non-linear systems of Type 1 and 2 (including stiff ones). See [3].

1.4 Expressions and Functions

The following functions and operators are supported for programming the systems mentioned above.


+ - * / ^	arithmetic operators: add, subtract, multiply, divide, power

exp(x)	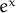$ex$

sqrt(x)	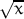$√x--$

log(x)	natural logarithm of x

log10(x)	common (base 10) logarithm of x

sin(x)	sine of x

cos(x)	cosine of x

tan(x)	tangent of x

asin(x)	arc sine of x

acos(x)	arc cosine of x

atan(x)	arc tangent of x

sinh(x)	hyperbolic sine of x

cosh(x)	hyperbolic cosine of x

tanh(x)	hyperbolic tangent of x

sinint(x)	sine integral of x 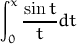$∫x sin t ----dt 0 t$

cosint(x)	cosine integral of x 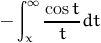$∫ ∞ cost- - t dt x$

sign(x)	sign of x 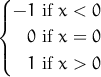$( \|{ - 1 if x < 0 0 if x = 0 \|( 1 if x > 0$

abs(x)	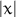$\|x\|$

iif(x,expr1,expr2)	immediate if 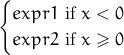${ expr1 if x < 0 expr2 if x ≥ 0$

sat(x,y)	satellite function of x and y 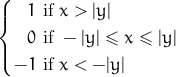$( \|{ 1 if x > \|y \| 0 if - \|y\| ≤ x ≤ \|y\| \|( - 1 if x < - \|y \|$

i	1 (one)

	0 (empty field means zero)

Examples: 2*sin(t-1)+cos(t)-x^2, sqrt(abs(x)), iif(t,sin(x),cos(x)) etc.

[next] [front] [up]

1 Introduction

1.1 What it does

1.2 Why Runge?

1.3 System Types and Solvers

1.4 Expressions and Functions