1 Введение

1.1 Что делает Рунге

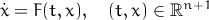
Рунге – это интерактивный решатель систем обыкновенных дифференциальных уравнений (ОДУ). Он решает задачи с начальными значениями (т.н. задачи Коши), которые могут быть определены следующим образом: для данной системы обыкновенных дифференциальных уравнений

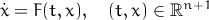
и данных начальных значений

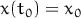
найти решение

для данного значения “времени”, т.е. для данного значения 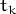независимой переменной 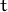. Рунге также вычисляет множество решений

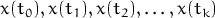
где – количество выполненных шагов. Это позволяет строить траектории решений.

1.2 Почему Рунге?

• Он быстрый. Рунге использует ФОРТРАН-библиотеки BLAS и LAPACK, оптимизированные для современных многоядерных процессоров.
• Он интерактивный. Рунге позволяет начинать решение щелчком мыши из точки на плоскости.
• Он точный. Рунге использует правило Рунге для выбора оптимальной длины шага, обеспечивающей заданную точность.
• Он эффективный. В том случае, когда нужно вычислять производные (например, элементы матрицы Якоби), Рунге делает это аналитически, т.е. не прибегая к разностным схемам.
• Он переносимый. Рунге работает на платформах Windows и Linux (32-х и 64-х разрядные версии) и Mac OSX (64-х разрядная версия).
• Он открытый. Рунге позволяет добавлять ваши собственные алгоритмы.
• Он лёгок в использовании. Рунге позволяет экспортировать решения в программы MS Excel и MATLAB.
• Он бесплатный. Рунге распространяется по свободной лицензии Boost Software License.

1.3 Типы систем и алгоритмы

Рунге поставляется с предустановленными алгоритмами, оптимизированными для решения систем следующих типов:

• Тип 1. Неавтономная система общего вида

• Тип 2. Автономная система общего вида (этот тип является подмножеством Типа 1, т.е. для автономных систем возможно использование обоих типов, что порой имеет смысл для более широкого выбора алгоритмов)

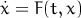
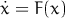
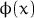• Тип 3. Псевдо-линейная система (здесь предполагается, что относительно мало по сравнению с )

• Тип 4. Псевдо-линейная система с постоянной матрицей B

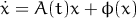
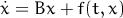
Следующие алгоритмы поставляются с программой:

• Runge-Kutta process modification developed by R. England. Быстрый и точный алгоритм 5-го порядка для решения систем 1-го типа. См. [1].
• Exponential method modification developed by J.D. Lawson. Рекомендуется для линейных и псевдо-линейных систем типов 1, 3 и 4 (включая жёсткие системы). Этот алгоритм А-стабилен для линейных систем, т.е. погрешности не зависят от длины шага. См. [2].
• Implicit process developed by H.H. Rosenbrock. Рекомендуется для нелинейных систем типов 1 и 2 (включая жёсткие системы). См. [3].

1.4 Выражения и функции

Следующие функции и операторы поддерживаются для программирования систем, рассмотренных выше.

+ - * / ^	арифметические операторы: сумма, разность умножение, деление, степень
exp(x)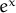
sqrt(x)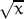
log(x)	натуральный логарифм x
log10(x)	логарифм x по основанию 10
sin(x)	синус x
cos(x)	косинус x
tan(x)	тангенс x
asin(x)	арксинус x
acos(x)	арккосинус x
atan(x)	арктангенс x
sinh(x)	гиперболический синус x
cosh(x)	гиперболический косинус x
tanh(x)	гиперболический тангенс x
sinint(x)	интегральный синус x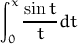
cosint(x)	интегральный косинус x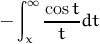
sign(x)	знак x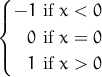
abs(x)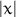
iif(x,expr1,expr2)	условный оператор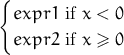
sat(x,y)	сателлит-функция x и y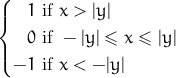
i	1 (единица)
	0 (пустое поле означает ноль)

Примеры: 2*sin(t-1)+cos(t)-x^2, sqrt(abs(x)), iif(t,sin(x),cos(x)) и т.д.